지수평활방법
- 선형이동평균에서 현재 시점의 시계열자료에 큰 가중치를 주고 과거로 갈수록 작은 가중치를 주는 것이 일반적이고 합리적인 가중치 패턴임
- 지수평활방법에서 과거로 갈수록 지수적으로 감소(exponentially decreasing)하는 가중치 패턴을 다루게 됨
단순지수평활방법(Single Exponential Smoothing: SES)
1) 주기가 N인 단순이동평균방법으로 예측값을 얻을 경우, 예측시점 T에서 시점 (T+1)의 예측값은 다음과 같이 1번식이 된다.
2) 만일 아주 과거의 시계열 값 Y(T-N)이 존재하지 않는다면, Y(T-N) 값 대신 시점 T의 예측값 F(T)로 대체한다. (2번식)

3) 단순이동평균방법인 (1번식)은 시계열자료가 정상적(stationary)일 경우 적절한 예측방법일 수 있으나, 계절성이 있거나 시계열에 추세가 있을 경우 좋은 예측값을 얻을 수 없다. 따라서 (1번식)은 기본적으로 시점(T+1)의 예측값을 예측시점(T)의 시계열 값(Y(T))와 예측시점의 계산된 예측값(F(T))의 가중평균한 것이다.
4) 주기(N)이 주어져 있지 않을 경우(또는 주기를 모를 경우)에는 (1번식)보다는 다음과 같이 임의의 가중치를 부여하는 것이 바람직하다.
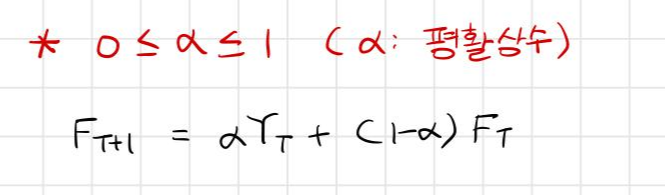
5) α는 (0, 1)사이의 값이므로 예측시점의 가중치보다 시계열의 과거값들에 점점 작은 가중치를 부여하는 패턴을 갖게 된다.
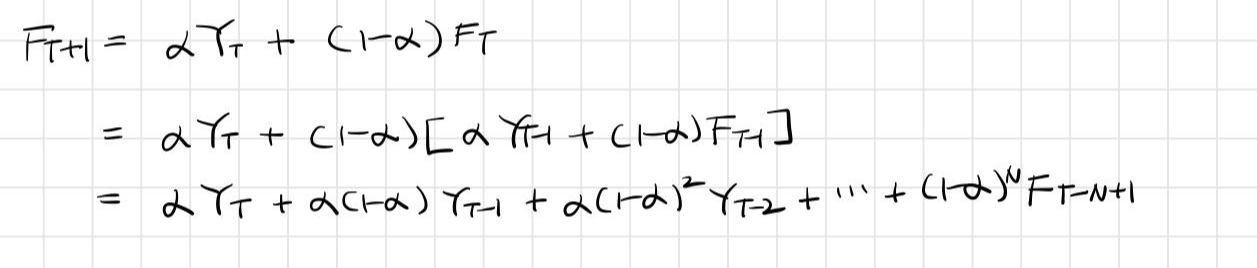
6) 식을 다음과 같이 표현하면 시점(T+1)의 예측값은 예측시점(T)에서의 예측값에 예측오차 (Y(T)-F(T))가 어느 정도 조정되어 얻어진다는 것이다. 알파(평활상수)가 1에 가까우면 예측오차가 많이 반영되는 예측값을 얻게 되고, 알파(평활상수)가 0에 가까운 값이면 이전 시점의 예측값과 비슷한 예측값을 갖게 되어 평활효과가 더욱 커진다는 점을 알 수 있다.

7) 초기값을 주는 방법
- 위 식을 이용하여 지수평활예측을 하기 위해서는 초기 평활값 F(1)가 주어져야 한다.
- F(1)의 처음의 4~5개의 관측값의 산술평균값을 사용
- 초기의 관측값을 사용 F(1) = Y(1)으로 하는 방법
- 전체자료의 평균 Y bar를 사용
=> 일반적으로 관측값의 수준이 급격히 변할 때 F(1) = Y(1)이고 변화의 폭이 완만할 때 5개의 산술평균(또는 표본평균 Y bar)을 이용
8) 적절한 α값의 이용
- α값이 1에 가까우면 최근 관측치에 더 가중치를 부여, α값이 0에 가까우면 과거 시점의 관측값에 가중치를 부여
- 자료 변동이 심하거나 패턴의 임의성이 보이면 α는 1에 가까운 큰 값을 사용, 자료가 안정적이고 변동이 완만한 자료에서는 작은값의 α 즉 0에 가까운 값 사용
- α는 주로 0.01과 0.30 사이의 값을 사용
- 적절한 α의 선택은 예측오차의 제곱합(SSE)을 최소로 하는 α를 선택 -> SPSS에서는 자동적으로 가장 적합한 α값의 예측값을 제공함
Brown 지수평활방법
1) Brown의 선형지수평활법은 추세성을 갖는 시계열의 예측을 위한 지수 평활법이다. 즉, 단순지수평활법에서 자료가 추세유형을 보이면 예측치와 관측치간의 차이를 갖게 되므로 이를 줄이기 위해 관측값과 평활값의 차이를 수정해야한다.
2) Brown의 선형지수평활법은 단순지수평활치를 한번 더 평활하여 이중지수 평활치(반복평활된 값)를 구하고 이를 이용하여 추세유형을 추정한 후 추정된 추세유형을 미래시계열의 예측치를 구하는데 이용된다.
=> 즉, 단순평활된 값들과 반복평활된 값들 모두 실제 자료들과 시차(lag)를 갖기 떄문에 단순평활된 값과 반복평활된 값의 차이를 단순평활된 값에 더하고 추세를 조정해주는 형태
3) Brown 방법의 예측모형

4) 계산의 예



Holt의 2-Parameter 지수평활방법(Holt의 선형지수 평활방법)
1) 추세변동비를 계산할 때 추세를 나타내는 식을 별개의 다른 평활상수 𝛾를 이용하여 평활을 시키므로 두 개의 평활상수를 갖는 평활방법이며, 이중지수 평활값을 사용하지 않는 것을 제외하고는 Brown의 방법과 유사한 방법이다.
2) Holt 방법은 추세를 나타내는 식을 다른 하나의 파라미터 𝛾로 평활하는 것이며, Holt 방법은 다음의 식들로 정의된다.

- 식 S(T)'의 뒷부분에 이전 싯점의 S(T-1)'에 이전 시점의 추세 b(T-1)을 더하여 조정하는 것을 볼 수 있음
- 식 b(T)는 추세를 평활해 나가는 것인데 추세가 잇을 경우 과거 값보다 크거나 작아지는 임의서이 있게되어서 S(T)' - S(T-1)'에 가중치 𝛾를 곱하고, 이전 시점의 추세 b(T-1)에 (1-𝛾)를 곱하여 합치는 것임
3) Holt의 2-파라미터 방법을 적용시키위 위한 초기값 결정은, S(1)' = Y(1)로 하면 되지만, b(1)을 결정시키기 쉽지 않다. 예를 들어 밑에 있는 벙븝 등으로 초기 추세값을 정할 수 있다. 이 초깃값은 시계열 자료의 특징을 보아 시행착오(trial-error)를 반복하면서 적절하게 결정해야한다.

Winter의 3-parameter 지수평활방법
1) 시계열자료가 정상적인 경우에는 이동평균방법이나 단순지수평활방법과 같은 방법들이 유용하게 사용될 수가 있다. 그러나 시계열 자료가 추세를 가지고 있는 비정상적 시계열자료라면 Brown의 방법이나 Holt의 방법을 적용하는 것이 바람직할 것이다. 하지만 추세를 가지면서 계절성이 있는 비정상적 시계열의 경우라면 Winter의 방법으로 예측하는 것을 고려해야한다.
2) 대부분의 월별 혹은 분기별 자료들은 계절변동을 포함하게 되므로 이러한 시계열에 대한 예측을 할 때는 계절변동을 고려할 수 있는 계절 지수 평활법을 사용해야 한다, 즉, 윈터스의 지수평활법은 추세와 계절유형을 동시에 보이는 자료를 지수평활방법으로 모형화하고 미래시계열을 예측하는 방법이다.
예시 ) 기업 A의 분기별 수출량 시계열자료



=> 어떤 기업의 분기별 수출량 시계열자료에 대한 단순지수평활방법과 Brown 방법에 대한 예측결과인데, 이 표에서 볼 수 있는 것과 같이 단순지수평활방법이나 Brown의 방법으로 예측된 값들의 예측오차들을 일정한 패턴을 갖는다는 점이다. 즉, 매 4분기의 예측 오차가 -의 값을 갖고 다른 분기들에서는 + 값을 갖는 것을 알 수 있다. 이것으로 볼 때 시계열자료가 뚜렷한 계절성을 갖고 있음을 알 수 있다. 따라서 이러한 시계열자료에 대해서는 계절성을 해결할 수 있는 Winters의 방법으로 접근하는 것이 바람직하다.
3) 윈터스의 지수평활법
- 가법적계절모형 : 시계열의 계절적 진폭(분산)이 시간의 흐름에 따라 일정한 경우에 사용
- 승법적계절모형 : 시계열의 진폭이 시간의 흐름에 따라 점차적으로 증가 혹은 감소하는 경우에 사용
승법적 계절지수 평활에 의한 예측모형
- 홀트의 선형지수 평활법을 확장시킨 방법으로 시계열이 선형추세성과 승법적 계절변동을 나타낼 때 적용하는 방법

- 계절조정요인 식 I(T)는 계절지수와 비교될 수 있는데, 현시점의 시계열자료를 현시점의 평활값으로 나누어 L이전 시점의 계절조정요인으로 조정한 것이다. Y(T) / S(T)'는 1보다 클 수도 작을 수도 있으며, 계절성을 나타내는 지수이다.
- 식 S(T)'는 Holt의 방법과 약간 차이가 있는데 시계열 자료 Y(T)를 L 이전의 시점의 계절조정 요인으로 나누어 줌으로써 계절성을 제거 시킨다. 즉, I(T-L)이 1보다 큰 경우라면 (T-L) 시점의 시계열 값이 평균보다 크다는 의미가 있기 때문에 Y(T)를 작게 조정해주는 효과가 있는 것이다.
- 초기값을 얻는 방법에는 추세를 나타내는 b의 초기값은 2개의 계절주기 자료들을 사용하여 계산할 수 있다.

가법적 계절지수 평활에 의한 예측모형
- 선형추세성과 가법적 계절변동을 갖는 시계열에 적용하는 방법

'통계공부 > 시계열분석' 카테고리의 다른 글
| 시계열 요소분해법 (2) (0) | 2021.04.16 |
|---|---|
| 시계열 요소분해법 (1) (0) | 2021.04.15 |
| 평활법 - 이동평균방법 (0) | 2021.04.14 |
| 시계열 자료의 예측 정확도 측정 (0) | 2021.04.13 |
| 시계열의 기본개념 및 변동요인 (0) | 2021.04.13 |
