이동평균방법
- 이동평균방법(Moving Average Method)란 어느 시계열 자료에 대해 예측시점(T)을 기준으로, 차기(T+1)의 예측값을 시점 T에서 가지고 있는 과거 자료의 평균값으로 하는 방법
- 대체로 일정한 주기를 갖고 비슷한 패턴으로 움직이고 있는 경우에 적용시킬 수 있는 방법
- 주기가 길어질수록 많은 자료로써 평균을 얻는 것이기 때문에 직선에 가까운 부드러운 선이 얻어짐
- 이동평균방법에는 평균방법, 단순이동평균방법, 선형이동평균방법 등이 있음
- 단순이동평균은 현재 시점에서부터 몇 시점 전까지의 자료로 구한 평균이므로 단순이동평균은 평활법보다는 예측목적으로 주로 사용되며, 평활의 목적으로 이동평균을 구하고자 할 경우에는 특히 계절조정을 하고자 할 경우에는 중심화 이동평균이 권장됨
단순평균방법
1) 시계열 자료, { Y(T) } 가 있을 때 예측시점(T)에서 차기시점(T+1)의 예측값, F(T+1)로 나타내고, 예측시점에서 가지고 있는 과거 자료들의 평균을 차기시점의 예측값으로 한다.

2) 평균을 예측의 방법으로 적용시킬 수 있는 시꼐열자료는 추세(trend)도 없고 계절성(seasonality)도 없는 시계열 자료가 적합
3) 단순평균방법에서 사용되는 자료의 수가 많으면 많을수록 안정적(stable)인 평균값이 얻어지기 때문에 평균을 이용할 경우 좋은 예측값 가능
4) 시계열자료가 추세나 계절성이 있을 경우 또는 어느 시점에 급격히 변화하는 모습이 나타낸다면 평균의 방법으로 좋은 예측값 기대 불가
=> 단순평균법은 관측된 모든 시계열자료를 이용해서 새로운 자료가 추가되어도 단순평균값에 크게 영향을 주지 못함, 따라서 가장 많이 영향을 주는 최근 자료의 정보가 예측에 기여하는 기여울이 상대적으로 낮아짐. 이러한 문제점을 보완하기 위해 단순이동평균법, 단순지수평활법등이 주로 사용됨
단순이동평균방법
1) 단순이동평균방법이란 시계열자료가 충분히 확보되어 있을 경우, 일정한 수의 자료들을 평균하여 예측하는 방법이다.
2) 최근 일정기간 동안(m:기간)의 시계열의 단순평균을 구하여 미래를 예측하는 방법이다.
3) 예측시점을 기준으로 과거 일정한 개수의 자료들 평균을 다음 시점의 예측값으로 사용하는 방법이다.
4) 예측시점(T)을 기준으로 과거 몇 개의 자료로써 평균을 얻는 주기(N)이 결정되면, 다음과 같은 방법으로 이동평균(Moving Average:MA)을 얻을 수 있다.

5) 위 표처럼 시점(T, T+1, T+2)에서 각각 시점 ( T+1, T+2, T+3)의 예측값 ( F(T+1), F(T+2), F(T+3) )을 얻는데 각 시점에서부터 과거 N개의 자료들을 평균하여 예측하는 방법이다.
6) 주기 N은 시계열의 성격에 따라 다양하게 결정가능하며, 주기가 N인 단순이동평균방법(PMA)을 MA(N)이라 표현한다.
7) 단순이동평균방법도 시계열자료가 추세를 갖고 있을 경우에 부적절하다.
8) 주기(N)의 고려사항
- MA(1)는 현재 시점(T)의 시계열 값으로 다음 시점(T+1)의 시계열 자료를 예측한다는 것
- MA(4)는 분기별 자료에 대해 사용할 수 있는데, 4개의 자료들 평균을 얻으면 분기마다 가지고 있는 계절효과가 제거됨
- 단순이동평균방법처럼 분기별로 나타나는 시계열자료의 평균값을 다음 시점의 예측값으로 한다는 것은 추세나 계절효과를 나타내기에 바람직하지 않음 --> 중심화 이동평균방법으로 시계열자료들의 요소 파악이 가능해짐
9) 많은 자료들의 평균을 내어서 예측값으로 사용한다는 것은 그 기간 동안의 크고 작은 값들이 많이 상쇄되기 때문에 주기를 크게 하면 할수록 시계열자료를 부드럽게 하는 효과가 있음

10) 시점 (T+2)의 예측값은 F(T+1)을 (Y(T+1) - Y(Y-(N-1))) / N만큼 조정한 것이라는 의미이고, 즉 N이 상당히 크다면 F(T+2)는 F(T+1)과 큰 차이를 보이지 않을 것이다.

중심화 이동평균방법
1) 단순이동평균방법에서는 주기가 3인 이동평균을 계산할 때, 시점 1-2-3의 이동평균값이 시점 4의 예측값이 되지만 계절적인 변동이 있을 경우 시점 1-2-3의 이동평균은 계절변동을 상쇄한 것이므로 이동평균값의 위치를 시점 1-2-3의 중심인 시점 2에 위치시는 것이 바람직한데 이를 중심화 이동평균방법이라고 한다.
2) 즉, 주기 N의 이동편균값의 위치를 N기간의 가운데로 이동하는 것이다.
3) N이 짝수인 경우 중심위치를 정할 수 없기 때문에 N/2번째 이동평균값과 N/2+1번째 이동평균값의 평균을 구하여 N/2+1번째 위치에 놓는다.
4) N이 홀수인 경우 이동평균값의 위치를 N/2번째 위치에 놓는다.
ex > 시점 1~4의 이동평균값과 시점 2~5의 이동평균값의 평균 시점 3에 위치시킴
비교
- 단순이동평균방법의 주기가 3, 5인 경우에서 시계열 자료의 예측결과이다.

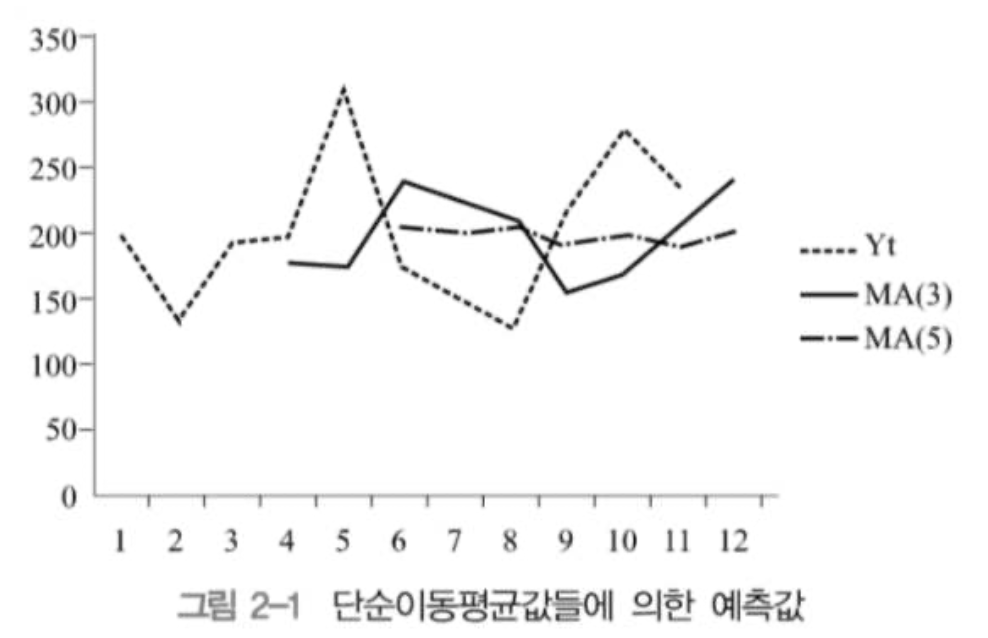

=> 주기가 큰 MA(5)가 MA(3)보다는 부드러운 예측값들의 곡선을 나타내고 있음을 볼 수 있고, 두 가지 예측방법의 여러 가지 정확도 값들을 비교해볼 때, 모든 척도 값에서 MA(5)가 MA(3) 보다는 척도가 작기 때문에 좋은 예측방법이라고 볼 수 있다.
- 중심화이동평균방법의 주기가 3, 5인 경우에서 시계열 자료의 예측결과이다.

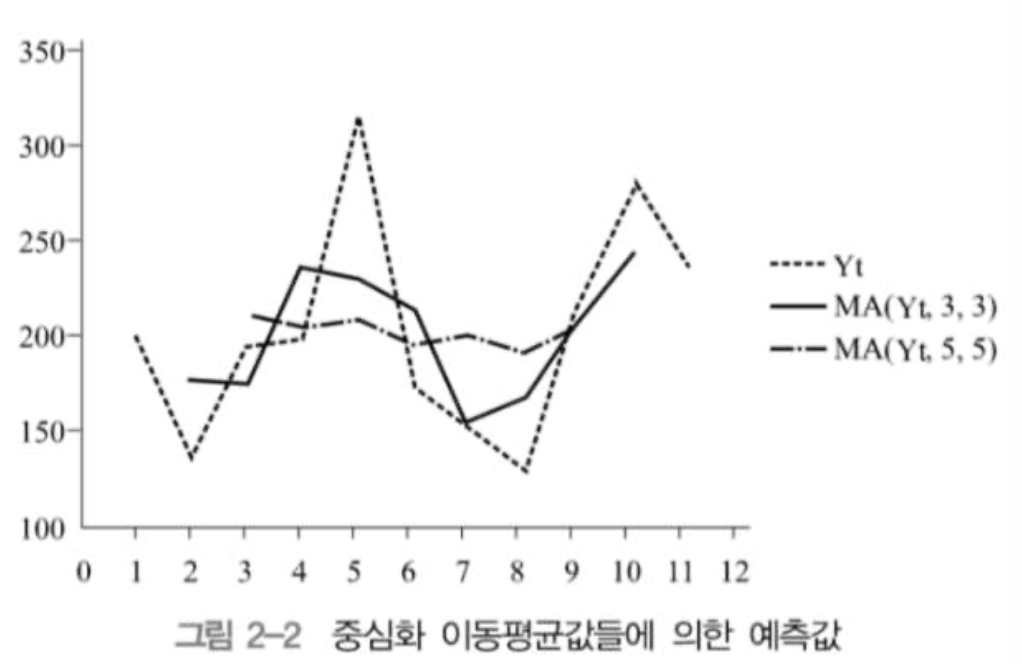
=> 이동평균의 주기를 5로 했을 때보다 3으로 했을 때 원 시계열자료에 접근되어 있는 예측값들이 얻어짐을 알 수 있고, 또한 중심화시키지 않은 경우보다도 훨씬 예측이 잘 되어 있는 것을 알 수 있다.
선형이동평균방법
1) 앞에 있는 방법들은 시계열자료가 어떤 추세를 보이고 있을 경우 적당한 예측방법이 될 수 없기 때문에 추세가 있는 경우 선형이동평균방법(linear moving average method)을 사용하는 것이 바람직하다.

=> 시점이 2만큼 증가하는 추세가 있는 경우 시계열자료 주기 3의 단순이동평균방법을 적용시켜 예측할 경우 오차가 동일하게 4가 나오고 이는 체계적 오차에 해당된다.
2) 선형이동평균방법은 이동평균값들을 다시 이동평균하여 얻어진 값들로 예측하는 방법이다. 따라서 선형이동평균방법을 반복(또는 이중)이동평균방법이라고 하며 주기가 N인 이동평균값들을 다시 주기 N으로 반복하여 이동평균하는 방법으로서, 그 결과를 MA(N X N)으로 표현한다.
3) 선형이동평균방법에 의한 예측방법을 일반화시키면 다음과 같다.

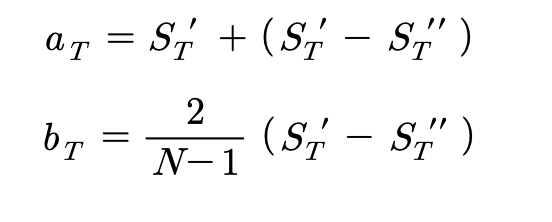
다음과 같이 할 때, 선형이동평균방법으로 시점 T에서 시점 (T+m)의 예측값은 다음과 같다.
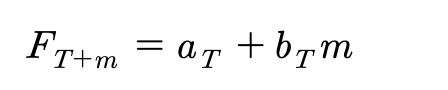
가중이동평균(이중이동평균)
1) 3x3 이중이동평균(3x3 가중이동평균) : 3기간 중심화 이동평균을 다시 3기간 중심화 이동평균한 것
2) 3x5 이중이동평균(3x5 가중이동평균) : 5기간 중심화 이동평균을 다시 3기간 중심화 이동평균한 것
3) 2x4 이중이동평균(2x4 가중이동평균) : 4기간 중심화 이동평균을 다시 2기간 중심화 이동평균한 것
=> 예시


'통계공부 > 시계열분석' 카테고리의 다른 글
| 시계열 요소분해법 (1) (0) | 2021.04.15 |
|---|---|
| 평활법 - 지수평활방법 (0) | 2021.04.15 |
| 시계열 자료의 예측 정확도 측정 (0) | 2021.04.13 |
| 시계열의 기본개념 및 변동요인 (0) | 2021.04.13 |
| 시계열 분석의 자료와 예측 (2) (0) | 2021.04.13 |
