Box-Jenkins 모형
1) Box-Jenkins 모형은 시계열자료 분석의 대표적인 예측모형이다. ARIMA(Auto-Regressive Integrated Moving Average) 모형으로 일컬어지는 Box-Jenkins 방법은 주어진 시계열자료가 어떤 모형에 맞을 것인가를 판단하고 시계열자료를 그 모형에 적용시켜 나가는 방법
2) Box-Jenkins 모형에 의하여 시계열 자료를 다룰 때 다음의 세 가지 단계를 거친다.
(1) 모형식별(model identification)
: 현시점을 기준으로 과거 시계열자료들로 부터 얻어진 여러 가지 통계량으로써, 그 시계열 자료가 어느 모형에 적합한 가를 알아보는 단계
(2) 식별된 모형의 파라메터(모수) 추정 및 진단(testing)
: 일단 어느 모형이라고 식별한 후에 시계열자료들로써 그 모형의 파라메터(모수)들을 추정한다. 추정된 모형으로부터 얻어진 예측값(또는 적합값(fitted-value)), 잔차들이 적합한가를 진단하는 단계이며 여기서 적합하지 않은 경우 다시 모형 식별을 해야함
(3) 예측(forecasting)
: 2단계에서 구해진 모형의 파라메터(모수) 값들을 이용하여 향후 시점에 대한 예측을 하는 단계
3) Box-Jenkins모형은 정상적 시계열에 대한 식별을 하는 것이기 때문에 비정상적 시계열자료를 분석해야 할 경우에는 비정상적 시계열을 먼저 정상적 시계열로 바꿔야 한다.
시계열과 확률과정
1) 시계열과 확률과정
- 임의의 시점 t에서의 시계열을 Zt(또는 Yt)로 표시하고 Zt(또는 Yt)를 하나의 확률변수(random variable)라고 하면 확률변수 Zt의 모집단으로부터 각 시점에서 얻어진 표본 즉, 실제로 관측된 자료를 실현값이라고 한다.
단위 : 년, 분기, 월, 일, 시, 분, 초 등...
- 확률변수들의 집합 { Zt, t=0, 1, 2, ..., n }를 확률과정(stochastic process)라 하고 특히, t가 시간을 나타낼 때 이 확률과정을 시계열과정(또는 시계열 모형)이라 한다.
- 확률변수 Zt는 하나의 분포를 가지며 실현값 Zt는 Zt가 취할 수 있는 값 zt(1), zt(2), ..., zt(n)들 중 하나이고 두 시점 t 와 s 에서의 확률변수 Zt와 Zs는 서로 종속이다.
2) 평균 및 자기상관함수
- 시계열 { Zt, t=0, 1, 2, ..., n } 에 대하여

=> 여기서 상관도(correlogram)은 자기상관함수를 그래프로 나타낸 것으로 시계열의 자기상관함수 구조를 일목요연하게 보여주기 때문에 모형수립과정에서 자주 이용된다.
3) 정상성
- 유한개의 관찰된 시계열자료로부터 모집단인 시계열모형에 관한 통계적 추정 및 검정을 하기 위해서는 분석을 단순화시키는 어떤 가정이 필요한데 이 중 가장 중요한 것이 정상성(Stationary)의 가정으로 이것은 시계열모형의 확률적 성질이 시간에 따라 변하지 않는다고 가정하는 것이다.
- 즉, 시계열의 평균과 분산이 시점 t에 관계없이 일정하고 공분산은 두 시점의 시차 k에만 영향을 받는다. 정상확률과정(stationary stochastic process)은 넓은의미의 정상을 갖는 확률과정이다.

4) 표본자기상관함수와 편자기상관함수
표본자기상관함수(SACF), 상관계수(AC)
자기상관함수는 관측된 시계열이 시간에 따라 독립인지 아닌지를 파악하는데 이용된다.

-> 자기상관함수는 동일한 변수를 시점을 달리하여 관찰했을 때 시점이 서로 다른 관찰값들 사이에 존재하는 상호관계를 나타낸 것
-> 예시
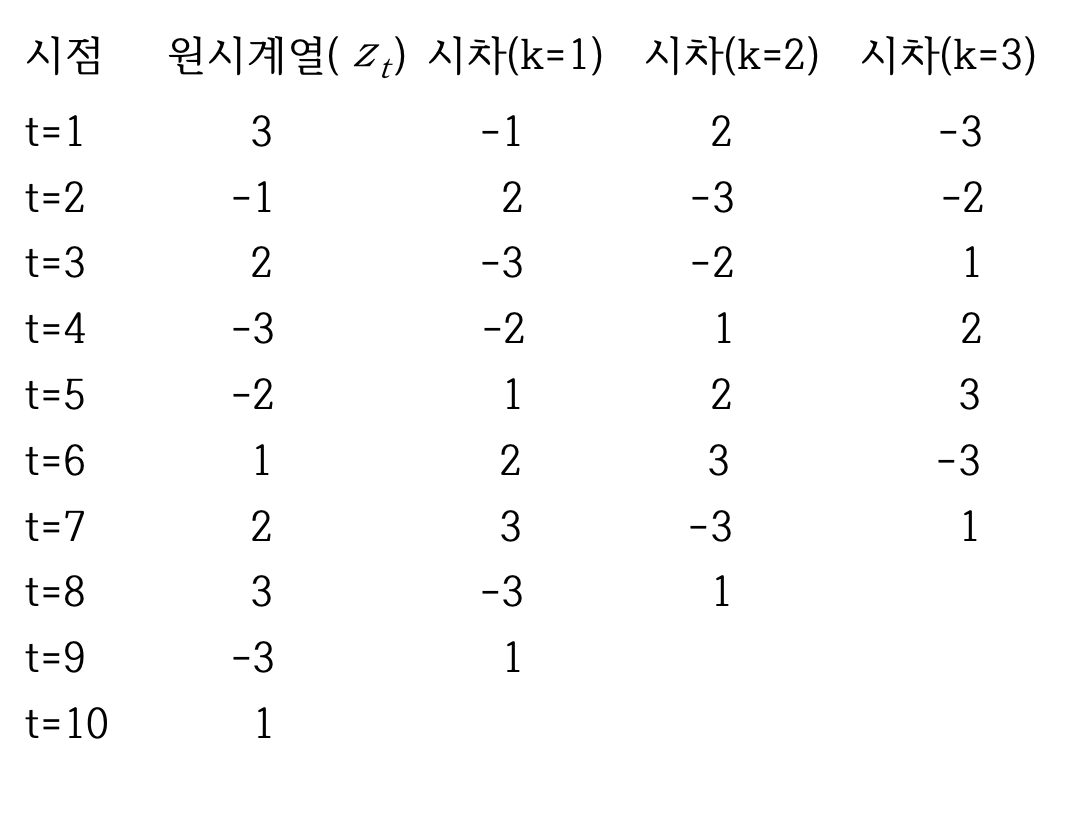
- 정상시계열 { zt }가 주어졌을 때

편자기상관함수(PACF), 편자기 상관계수(PAC)
자기상관함수와 더불어 모형의 식별에 이용된다.
- 임의의 시차 k에 대하여 z(t)와 z(t-k)의 상관관계에서 그것들 사이에 끼어있는 z(t-1), z(t-2), ... , z(t-(k-1))의 상호선형의존성을 제거한 후의 z(t)와 z(t-k)만의 자기 상관함수를 편자기상관함수(partial autocorrelation function)이라 한다.
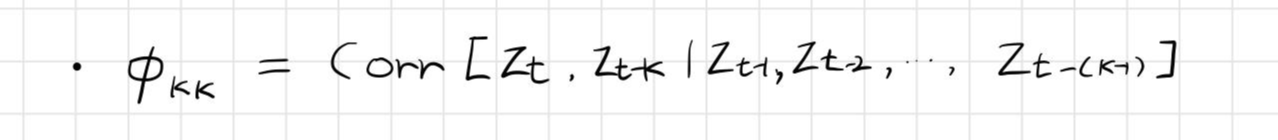
- 시차가 k인 편자기상관함수는 평균이 0인 정상시계열 {z(t)}에서



정상시계열 모형
백색잡음모형
- (정의) 정상확률과정중에서 서로 독립이고 동일한 분포를 따르는 (iid) 확률변수들의 계열로 구성된 확률과정을 백색잡음과정(white noise process)라 한다.
- 대부분의 시계열모형은 백색잡음으로부터 얻어지기 떄문에 기본적인 모형이라고 할 수 있다.
- 백색잡음과정의 모형

- 백색잡음모형의 시계열도표


-> 백색잡음의 시계열도표는 시계열이 평균 0을 중심으로 특정한 패턴없이 랜덤하게 분포한다. 즉, 이 시계열들은 백색잡음모형을 따른다고 할 수 있다.
- 백색잡음과정은 시계열 모형의 수립에 매우 중요하며, 다음이 성립되야 한다.



-> 시계열자료에 대해 자기상관함수와 편자기상관함수를 구하면 다음과 같은 결과를 볼 수 있다. 두 시차에서 신뢰한계(표준편차 2배)이내에 존재하므로 자기상관함수와 편자기상관함수 모두 백색잡음모형의 자기상관함수와 편자기상관함수의 성질을 만족한다.
'통계공부 > 시계열분석' 카테고리의 다른 글
| Box-Jenkins 모형 (3) - MA모형, AR모형, ARMA모형 (0) | 2021.06.08 |
|---|---|
| Box-Jenkins 모형 (2) - 정상적 시계열에 대한 Box-Jenkins 모형 (0) | 2021.06.08 |
| 시계열 요소분해법 (2) (0) | 2021.04.16 |
| 시계열 요소분해법 (1) (0) | 2021.04.15 |
| 평활법 - 지수평활방법 (0) | 2021.04.15 |
