정상적시계열에 대한 Box-Jenkins 모형
시계열의 자료가 정상적 시계열인 경우, Box-Jenkins 방법은 그 시계열 자료를 다음의 기본적인 세 가지 모형으의 하나라고 전제한다.
1) 자기회귀모형(AR: Auto-Regressive Model)
2) 이동평균모형(MA: Moving Average Model)
3) 자기회귀이동평균모형(ARMA: Auto-Regressive Moving Average Model)
자기회귀모형
1)
시계열의 모형에서 현시점의 상태를 과거시점의 상태들, 즉 과거의 자기자신의 관측값과 현시점의 오차의 함수로 나타낼 수 있다면

함수 f를 회귀함수라고 하고, 이 모형을 자기회귀모형(autoregressive model)이 된다.
(정의) 만일 Y(t)가 임의 정수 p에 대하여 Y(t-1), Y(t-2), ... , Y(t-p)만의 선형결합 즉, t-p차 까지만 영향을 받는다면
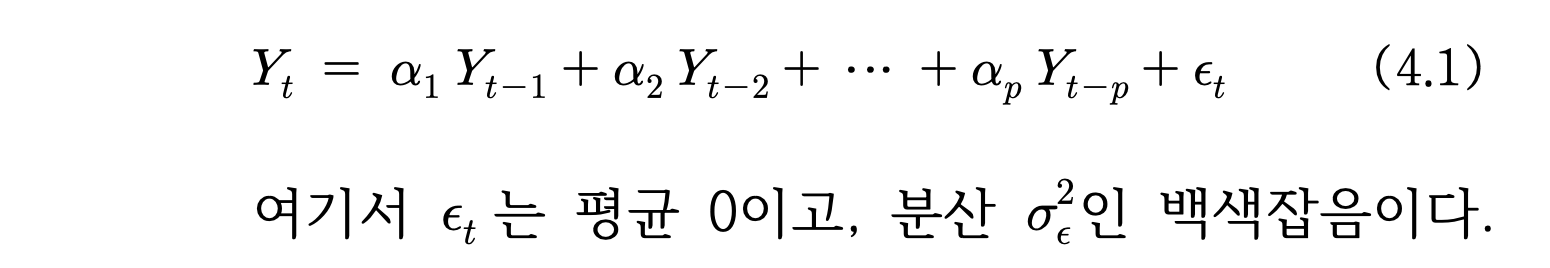
p차 자기회귀모형(Autoregressive model)이라 하고 AR(P)로 표시한다.
2) AR(1)모형 (1차 자기회귀모형)
- AR(1) 모형
AR(P)에서 P=1인 모형으로

이고, 현재의 관측지 Y(t)는 오직 앞 시점의 Y(t-1)에만 의존하며, 여기의 오차에서는 시점에 관계없이 독립적이고 정규분포를 가정한다.

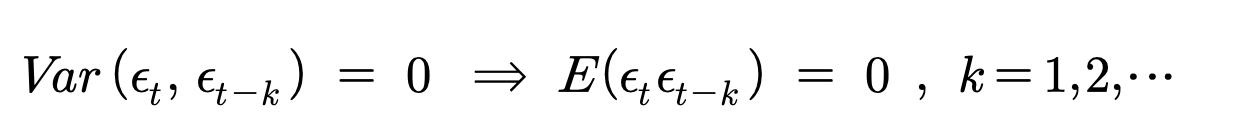
즉, 위 식이 성립되는 것이다.
- AR(1)과정의 정상성 조건

- AR(1)모형의 자기상관함수와 편자기상관함수
AR(1)모형의 자기상관함수(ACF)는

시차 k가 증가함에 따라 지수적으로 일정하게 감소하거나 부호가 바뀌면서 감소한다

AR(1)모형의 편자기상관함수(PACF)는

2) AR(2)모형 (2차 자기회귀모형)
AR(2)모형은 AR(p)에서 p=2인 모형으로

3) AR(p)모형 (p차 자기회귀모형)
p차 자기 모형 AR(p)모형은
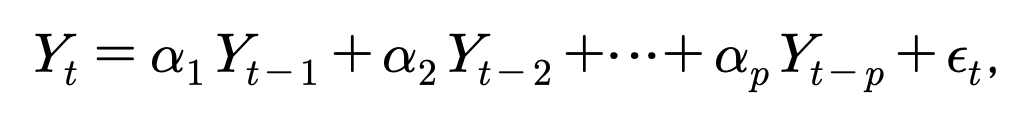
이동평균모형
1) (정의) 이동평균모형(moving average model)이란 시계열자료가 연속적인 오차항들의 영향을 받는다는 것이며,
q차 이동평균과정 MA(q)의 모형식은

으로 표현되는데 이 식을 q차 이동평균모형이라고 부르며 MA(q)로 나타낸다
2) MA(1) 모형
바로 이전 시점 (t-1)의 오차항만이 포함되는 경우라면 1차 이동펴균이 되며 식은 다음과 같다.

3) MA(2) 모형

4) MA(q) 모형

5) MA(q)모형의 가역성조건(Invertibility condition)
- 모형적합을 위해 모형과 ACF와의 일대일 관계를 성립시키기 위해 제약조건이 필요
- MA모형의 경우 β와 1/β인 경우 ACF가 동일한 형태가 나오게 되어 ACF를 이용해서 모형결정이 어려움
- 따라서 모형결정을 위해 MA모형을 AR(∞)모형으로 변환할 때 AR(∞)모형의 수렴조건을 MA모형의 가역성조건이라 함
- AR(∞)모형이 수립하기 위해 -1<α<1 이어야함
자기회귀이동평균모형
시계열자료가 과거의 시계열자료 값들과 과거의 오차값들 모두의 영향을 받을 때 AR과 MA가 혼합된 자기회귀이동평균모형(Autocorrelation Moving Average Model)을 다음과 같이 나타낸다.

1) ARMA(1, 1)모형
-가장 단순한 ARMA모형은 바로 이전 시점의 Y(t-1)과 오차만을 모형에 포함시켜 다음과 같이 ARMA(1, 1)를 표현한다.

2) ARMR 모형의 표현 방법
- ARMA모형은 AR모형과 MA모형의 혼합모형으로, 모든 AR모형이나 MA모형을 ARMA모형 표현 방식으로 나타낼 수 있다.
=> 예를 들어 AR(1)은 ARMA(1, 0)으로 MA(1)은 ARMA(0, 1)등으로 표현한다.
- 시계열자료(Y(t))의 평균(상수항)을 나타내는 방법
Y(t)와 Y(t-1)의 평균이 모두 μ인 자기회귀모형으로 정상적 시계열이므로 AR(1)모형은 정상적으로

모형식별
- 정상적 시계열에 대한 모형은 AR, MA, ARMA 세 가지가 있고 이 모형들에 대해 차수(order)를 결정해야 함
- 주어진 시계열자료를 어떤 모형에 적합시키는 것이 바람직한가를 식별(identification)이라 함
- 즉, 주어진 시계열자료로부터 얻어지는 통계량들을 수단으로 하여, 그 시계열자료는 AR, MA, ARMA 중에서 어떤 모형이며 차수는 얼마인가를 식별하게 되는데, 식별은 주어진 시계열자료로 부터 얻어지는 자기상관계수(ACF)와 부분자기상관게수(PACF)를 가지고 수행함
1) 자기상관계수(ACF)
- 자기상관계수(autocorrelation)란 주어진 시계열자료 Y(t)들의 정해진 시차간의 상관계수
- 시차 1의 자기상관계수는 다음식,



2) 자기상관계수의 분포
- 시계열자료 { Y(1), Y(2), ..., Y(T) }로부터 계산된 자기상관계수가 유의적인가를 알기위해서는 자기상관계수들의 분포를 알아야 한다.
- 즉, H0 : ρk = 0를 검증하기 위해서 rk의 분포를 알아야 하며 H0가 기각될 경우 얻어진 k차 자기상관계수가 유효한 것이라는 것이다.
가설 검증을 위한 검증 통계량 k차 자기상관계수인 rk의 분포는
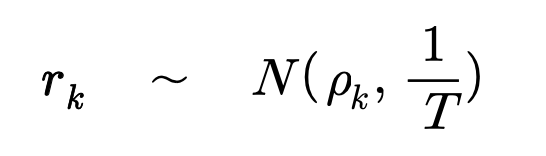
3) Box-Ljung Q* 통계량을 이용한 자기상관 검증
- 시차1에서 시차m까지 모든 자기상관계수들이 0인가를 판단하는 통계량으로 Box-Ljung Q* 통계량이 사용되는데 AR모형과 MA모형을 ARMA(p, q)로 표현했을 경우 통계량 값을 다음과 같이 얻어진다.

- Q* 통계량은 H0: ρ1 = ... = ρm = 0의 가설을 검증하는데 이용된다.
4) 부분자기상관계수(편자기상관함수:PACF)
- 자기상관계수 이외에 모형을 식별하는 또 다른 하나의 수단이 부분자기상관계수이다.
- 부분자기상관계수는 다중회구분석모형에서 반응변수 Y를 X1, X2에 회귀시킬 경우

의 모형에서, X2가 Y에 미치는 영향을 제외시킨 후 X1이 Y에 미치는 영향을 얻고자 할 때의 부분결정계수(부분상관계수의 제곱)이라는 개념과 유사하며, 시계열분석에서도 이와 같은 개념으로 부분자기상관계수를 이해하면 된다.
- 편자기상관계수(부분자기상관계수, PACF)란 시차가 주어졌을 때, 다른 시차들의 시계열자료 값들이 주어진 시차의 시계열자료 값들에 미치는 영향을 제거한 후에 주어진 시차에 대한 시계열자료들 간의 상관계수를 편자기상관계수(PAC, PACF)부분자기상관계수라고 한다.
- 즉, 임의의 시차 k에 대하여 z(t)와 z(t-k)의 상관관계에서 그것들 사이에 끼어있는 z(t-1), z(t-2), ..., z(t-k)의 상호선형의존성을 제거한 후의 z(t)와 z(t-k)만의 자기상관함수를 편자기 상관함수(partial autocorrelation function)이라 한다.

=> 주어진 시계열자료가 Box-Jenkins 모형 중 어느 모형으로 식별될 수 있는 가를 판단하는데 자기상관계수(ACF)와 부분자기상관계수(PACF)를 사용한다.
- MA모형 : 시계열자료의 ACF가 돌출적인 값들을(spikes) 갖고, PACF는 순차적으로 시나브로 작아지는(decay) 모습을 나타내는데, 유의적인 ACF의 spike 수로 MA 모형의 차수를 결정한다.
- AR모형 : MA모형과 달리 주어진 시계열자료의 PACF가 돌출적인 값들을 갖고, ACF는 순차적으로 작아지는 모습을 나타낸다. AR모형으로 판단되면 유의적인 PAC의 spike의 수로 차수를 결정한다.
- ARMA모형 : ACF와 PACF 모두 순처적으로 작아지는 경우, ARMA모형으로 식별되며 차수는 대체로 (2, 2)를 넘지 않는다. 즉, ACF와 PACF의 유의적인 spike 수가 각각 2를 넘지 않는다.
'통계공부 > 시계열분석' 카테고리의 다른 글
| Box-Jenkins 모형 (4) - 시계열의 모형구축 (0) | 2021.06.08 |
|---|---|
| Box-Jenkins 모형 (3) - MA모형, AR모형, ARMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (1) (0) | 2021.04.16 |
| 시계열 요소분해법 (2) (0) | 2021.04.16 |
| 시계열 요소분해법 (1) (0) | 2021.04.15 |
