모형의 파라메터 추정과 진단
시계열의 모형구축
(1) 시계열 모형구축하는 과정
- 모형식별단계 : 시계열의 도표를 그려 시계열의 특성을 파악하고 모형을 식별
- 모형추정단계 : 식별된 모형의 모수를 추정
- 모형진단단계 : 추정된 모형을 진단
- 모형설정단계 : 최종적인 모형 설정
- 예측단계

1) 시계열의 사전조정 : 추세의 제거, 분산안정화 변환
1. 추세성의 제거
- 결정적추세(deterministic trend) : 시간의 흐름에 따라 추세가 변하지 않고 일정하게 계속되는 것으로 차분을 통해서 추세를 제거하는 것보다 추세요인을 모형에 포함시켜 추세성분을 추정하고 예측에 사용
- 확률적추세(stochastic trend) : 인접 자료들간에 강한 양의 상관관계 때문에 어떤 추세가 있는 것처럼 보이는 경우가 있는데 이러한 추세를 확률적추세라고 하며, 자기상관함수가 모든 시차에서 완만하게 감소하는 모습을 보이며 이것을 차분을 통해 제거함
- 확률적 추세를 가지고 있는 비정상 시계열은 차분법을 통해 정상적 시계열로 변환할 수 있다.

- Yt에 대한 1차 차분식

- Yt에 대한 2차 차분식

* 차분을 수행할 때 과다차분에 주의 !!
과다차분 ? 선형췌스이 경우 1차 차분을 통해서 추세 성분이 제거되며, 차분된 시계열의 시계열도표와 자기상관함수를 다시 그려보고 시계열의 정상성 여부를 판단한다. 하지만 정상화된 시계열에 대해서 다시 차분을 실시하는 것을 과다차분이라 한다.
2. 분산안전화 변환
- 비정상시계열에 대해서 멱급수 변환과 같은 변수변환을 통해 시점에 관계없이 분산이 동일한 시계열을 얻을 수 있다. 이러한 분산안전화 변환은 양의 값을 갖는 시계열에만 적용되며, 다른 변환에 앞서 가장 우선적으로 실시하는 것이 바람직하다.
2) 모형식별
- 모형식별은 ARIMA(p, d, q)모형의 차수 p, d, q를 결정하는 것
- 모형식별을 위해서 이용되는 기준은 자기상관함수(ACF), 편자기상관함수(PACF), 확장된 표본자기상관함수(ESACF), 아카이케정보판단기준(AIC), SBC, BIC 등 존재
- 잠정적인 시계열 모형을 설정할 때는 가능하면 시계열 모형의 차수 p와 q의 값이 2를 넘지 않게 하는 것이 좋음
1. 자기상관함수와 편자기상관함수를 이용한 모형식별
- 백색잡음모형, AR(p), MA(q), ARMA(p,q), ARIMA(p,d,q)
2. 여러 가지 모형식별 방법
- 아카이케정보판단기준(AIC)

=> 잠정적으로 설정된 모형들이 여러 개가 있는 경우 각 모형들의 AIC값을 계산해 가장 작은 값을 갖는 모형을 선택
- SBC(Schwarz's Bayesian Criterion)

=> 여러 개의 설정된 모형에 대하여 가장 작은 SBC값을 제공하는 모형을 선택
- 확장된 표본자기상관함수(Extend Sample ACF: ESACF)
: ARMA(p, q)모형을 AR(p)모형으로 적합시킨다면 MA(q)부분이 잔차로 남아있게 된다. 이 경우 추정된 잔차는 백색잡음을 따르지 않고 MA(q)형태를 보이므로 모형적합단계에서 MA(q)부분을 모형에 포함시켜서 다시 모형을 적합시키고, 잔차분석을 통해 추정된 잔차가 백색잡음의 성질을 따르는가 본다. 만약 잔차가 백색잡음의 성질을 따르지 않고 특정한 모형을 보인다면 이를 다시 모형에 포함시켜 모형을 적합시키는 방법으로 잔차가 백색잡음의 성질을 만족할 때까지 반복적으로 모형을 개선해나가는 방법
3) 모수추정
1. 조건부 최소제곱추정법
MA모형과 ARMA모형의 경우 적률추정법에 의한 추정은 그 과정이 복잡하고 추정량 또한 유효추정량이 되지 못하며, 이 경우 조건부 최소제곱법을 이용하면 모수의 유효추정량 또는 일치추정량을 구할 수 있다.
2. 비조건부 최소제곱추정법
조건부최소제곱법에서 가정은 자료의 수가 크지 않을 경우나 계절시계열 모형에서는 추정값에 영향을 미치게 된다. 따라서 초기값을 지정하지 않고 오차 제곱합을 최소화시키는 방법이다.
3. 최우추정법
시계열의 결합밀도함수인 우도함수를 정의하고 우도함수값을 최대화시키는 모수를 구하는 방법이며, 백색잡음의 분포는 평균이 0, 분산이 σ^2인 정규분포를 가정하여 모형에 포함된 모수들의 추정치를 구하는 방법이다.
=> 모형의 파라메터(모수) 값들이 추정되면, 시계열 자료가 그 모형에 얼마나 잘 적합되는지를 판단해야한다.
4) 모형진단
1. 잔차 분석
2. 과다적합분석
5) 예측
평균제곱오차(MSE)

을 최소로 하는 값을 예측값으로 사용하는 방법이다.
(2) 적합도가 좋은 모형임을 측정하는 통계량
1) 작을수록 잘 적합하는 통계량
- 평균제곱오차제곱근(RMSE)


- 평균절대백분위오차(MAPE) : 잔차의 실제 자료에 대한 비율의 절댓값들 평균
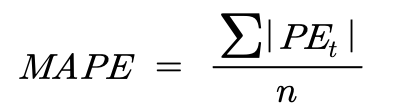

- 평균절대오차(MAE) : 잔차들의 절댓값들의 평균

- 절대퍼센트오차의 최댓값(MaxAPE)
- 절대오차의최대값(MaxAE)
- AIC, SBC



- 정규화된 BIC

2) 클수록 잘 적합하는 통계량
- R제곱, 정상 R제곱
(3) 잔차들의 자기상관 진단
- 시계열의 분석에서도 예측오차(잔차)들을 분석해야 하는데, 잔차들은 아무런 패턴을 갖지 않고 임의로 퍼져 있는 것이 바람직
- 잔차들로써 그래프를 얻었을 때 일정한 패턴을 보이거나 증가(또는 감소하는) 패턴을 보인다면 식별된 모형은 적당한 모형이 아님
- 즉, 오차항에 대한 가정(백색잡음)이 만족되어야함
- 시계열자료를 분석할 때 예측오차(잔차)들에 대한 진단에서 가장 중요한 것은 잔차들이 서로 상관되어 있는가를 알아보는 것이며 이러한 분석에는 Box-Ljung Q* 통계량을 사용
1) Box-Ljung Q* 통계량(자기상관이 존재하는가를 검증하는 통계량)
- 원래 Box-Pierce Q 통계량은 시차 묶음들에 대해 자기상관이 존재하는가를 검증하는 통계량이지만, Q통계량의 경우 n이 작은 경우 Q의 값이 너무 작아서 실제로 모형이 잘 적합되지 않았는데도 귀무가설을 기각하지 못하는 경향이 있다. 이러한 문제를 개선하기 위해 Box-Ljung Q* 통계량을 사용한다.
- Q* 통계량은 H0: ρ1 = ... = ρm = 0의 가설을 검증하는데 이용되며, 물론 Q* 통계량이 H0를 기각할 수 없어야하며(유의확률 p보다 커야함) 그 모형이(최적이 아니더라도) 주어진 시계열 자료에 적합한 모형이 되는 것이다.
- 이때 Box-Ljung Q* 통계량은 Box-Pierce 통계량을 개선한 것으로서 다음과 같이 정의된다.

이때 Q*는 자유도 (m-p-q)의 카이제곱분포를 따르며, Q* >= χ2(m-p-q)이면 유의수준 α에서 귀무가설을 기각하게 되고, 적합된 모형은 시계열 자료를 잘 설명하지 못한다고 할 수 있다.(H0을 기각할 수 없어야 모형이 잘 적합한다고 한다.)
(4) 추정된 파라메터(모수)들의 상관계수
- 파라메터의 수가 2개 이상인 모형에 대해서 추정된 파라메터들 간의 상관계수를 살펴야 함
- 만일, 두 개의 파라메터들 간에 높은 상관관계가 존재한다면 둘 중 하나의 파라메터는 제외시켜 모형을 간결하게 하는 것이 바람직
'통계공부 > 시계열분석' 카테고리의 다른 글
| 비정상적계절시계열모형(1) - 순수계절시계열 (0) | 2021.06.08 |
|---|---|
| Box-Jenkins 모형 (5) - 비정상적 시계열, ARIMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (3) - MA모형, AR모형, ARMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (2) - 정상적 시계열에 대한 Box-Jenkins 모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (1) (0) | 2021.04.16 |
