비정상적 계절시계열모형
- 시계열자료는 정상적 시계열과 비정상적 시계열로 나누어 지며, 모형 식별은 정상적 시계열에 대해 적용시키는 것이기 때문에 분석하고자 하는 시계열자료가 비정상적 시계열일 경우 차분을 한다거나 함수관계로 표현한 후 차분을 하는 방법 등으로 비정상적 시계열을 정상적 시계열로 전환시켜야함
- 그 후에 예측의 절차(추정 - 진단 - 예측)을 밟아나가는 것
- 지난 번에 배웠던 ARIMA모형이란 용어는 비정상적 시계열자료에 대해서 분석을 하는 경우의 모형에 대한 것이며, 정상적 시계열에 대한 모형을 ARMA모형으로 표현하는 것과 같이 비정상적 시계열자료에 대해서 ARIMA 모형으로 표현하는 것
- 우리가 분석하고 하는 시계열자료은 대부분 비정상적 시계열일 뿐만 아니라 계절성을 갖고 있으므로 이러한 계절성이 있는 시계열자료에 대해서 어떻게 다뤄야 하는지를 알아야 함
Integrated 모형 (차분된 모형)
(1) 원래 시계열자료 {Yt}를 차분했을 때에 얻어지는 정상적 시계열을 {Zt}로 표현하면 차분된 정상적 시계열인 {Zt}에 대해서 다음과 같이 3가지 모형으로 식별될 수 있을 것이다.
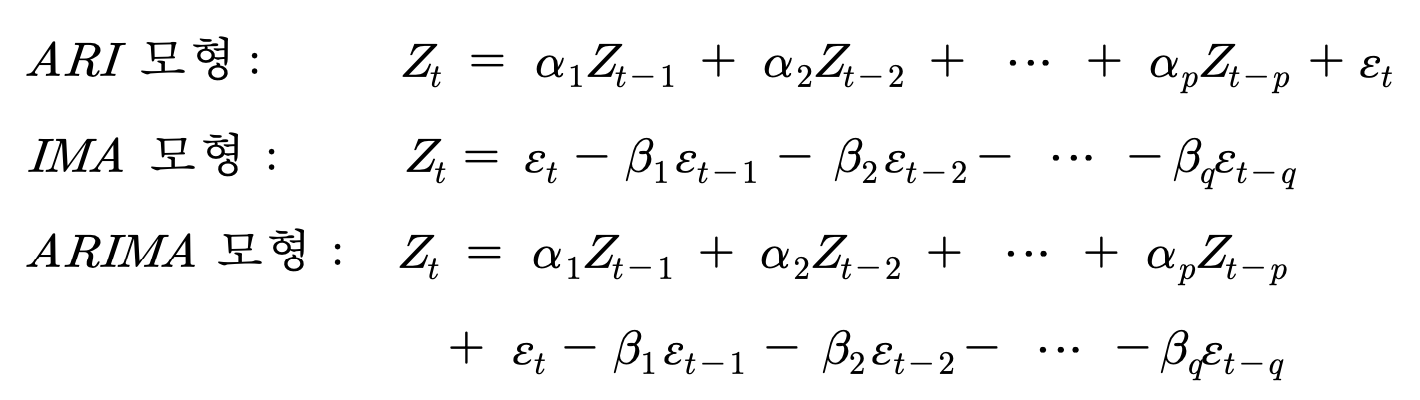
-> 정상적 시계열에서 위와 같은 모형을 ARIMA(p, d, q)라고 표현하는데 p는 AR의 차수, d는 차분의 차수, q는 MA의 차수를 나타내며, Box-Jenkins 모형은 모두 ARIMA(p, d, q) 모형으로 표현될 수 있다.
계절시계열
: 시계열자료가 일정한 시가 간격(주기)로 일정한 형태를 반복하고 있을 때, 계절시계열이라고 하며, 시계열자료란 시간의 흐름에 따라 얻어지는 자료이기 때문에 시간의 단위 일, 주, 월, 분기 등에 따라 계절성을 갖게 되는 경우가 대부분이다.
(1) 정상적 순수 계절시계열
1) (정의)
시계열자료가 정상적이면서 계절성만을 갖고 있을 경우 순수계절시계열(pure sea-sonal time series)라고 하며, 이때 주기를 s라한다.
즉 분기별 시계열자료일 경우 주기는 대개 4가 되며, t시점의 자료는 (t-4) 시점의 자료에 직접적으로 관련이 있다.
2) 계절주기가 s 인 순수계절시계열자료들의 AR, MA, ARMA 모형들

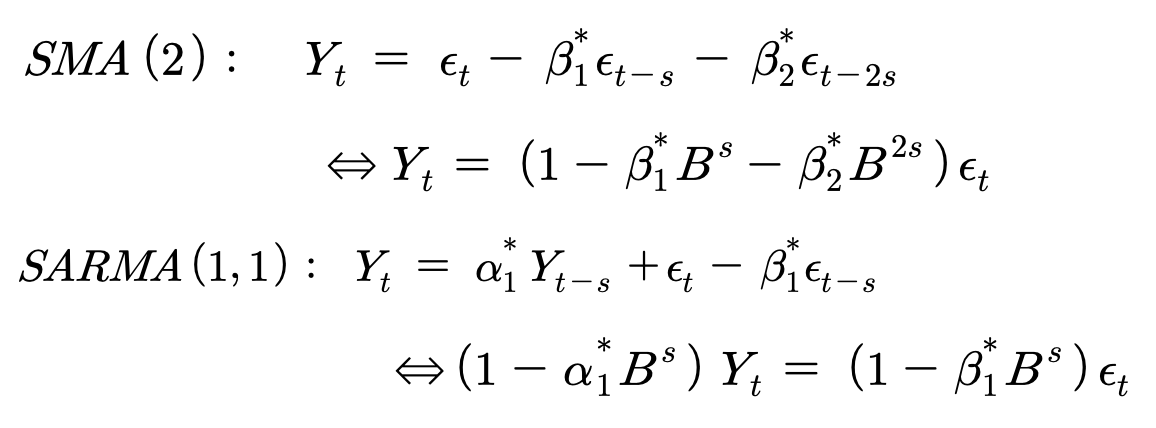
- 위에서 파라미터에 * 표시 한 것은 순수계절시계열에 대한 파라미터를 표현하는 방법이다.
- 후진연산자를 사용하여 계절성의 주기를 나타내는 방법을 사용하여 후진연산자의 상 첨자에 주기 (B^s)를 표현한다. SAR(2), SMA(2)모형의 차수들이 (t-s), (t-2s)인 것임을 유의한다.
3) 순수계절시계열의 ACF, PACF
계절 SMA(1), s=12 모형의 ACF와 PACF
- SMA(1), s=12 모형

1. Yt는 12개월 전의 오차와 관련이 있으므로
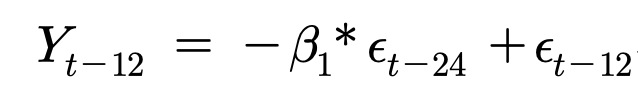
와 자기상관관계가 있어 자기상관계수가 얻어진다는 것을 쉽게 알 수 있다.
2. 나머지 시차들, (t-1), (t-2), ... 등에서의 오차항들은 서로 독립이므로 자기상관계수가 0이다.
3. 따라서 SMA(1) 모형일 경우 ACF는 시차 12에서만 유의한 값을 가진다.
- SMA(1), s=12 모형의 ACF
자기상관함수는 시차 12에서만 유의적인 값을 갖고 절단형태를 보인다.

- SMA(1), s=12 모형의 PACF
편자기상관함수는 지수적으로 감소하거나 진폭이 줄어드는 sine형태를 보이고 있으나, 계절 주기 s의 배수(s, 2s, 3s, ... )에 해당하는 시차에서만 나타난다.
- SMA(1), s=12 모형의 ACF

- SMA(1), s=12 모형의 ACF와 PACF 예시


계절 SMA(2), s=12 모형의 ACF와 PACF
- SMA(2), s=12 모형에 대한 ACF 그래프는 시차 12와 14에서만 유의적인 ACF가 나타난다

- 자기상관함수는 시차12, 24에서만 유의적인 절단형태를 보이며 편자기상관함수는 지수적으로 감소하거나 진폭이 줄어드는 sine 형태를 보이고 있으나 계절주기 s의 배수 (s, 2s, 3s, ... )에 해당하는 시차에서만 나타난다.
계절 SAR(1), s=12 모형의 ACF, PACF
- ACF가 점차적으로 작아지는 형태를 갖게 되는데, 다음은 SAR(1) , s=12 모형에 대한 ACF 그래프이다.

- 주기의 12의 배수 시점에서 점진적으로 작아지는 ACF 값들의 패턴을 볼 수 있다.
- 즉 자기상관함수는 계절 주기 s의 배수에 해당하는 시차 (s, 2s, 3s, .. )를 따라서 지수적으로 감소하는 형태를 보이며, 편자기상관함수는 시차가 s일 때 α1*의 값을 가지지만 그 외의 시차에서는 0의 값을 갖는 절단형태를 띠고 있다.
- 계절 SAR(1), s=12 모형의 ACF와 PACF의 예시

계절 SAR(2), s=12 모형의 ACF, PACF
- 자기상관함수는 계절주기 s의 배수에 해당하는 시차(s, 2s, 3s, ... )를 따라 지수적으로 감소하거나 진폭이 줄어드는 sine 형태를 보이며 감소하며 편자기 상관함수는 시차가 s, 2s에서 유의한 값을 갖고 그 이후 시차에서는 0의 값을 갖는 절단된 형태를 보인다.
- 계절 SAR(2), s=12 모형의 ACF와 PACF의 예시

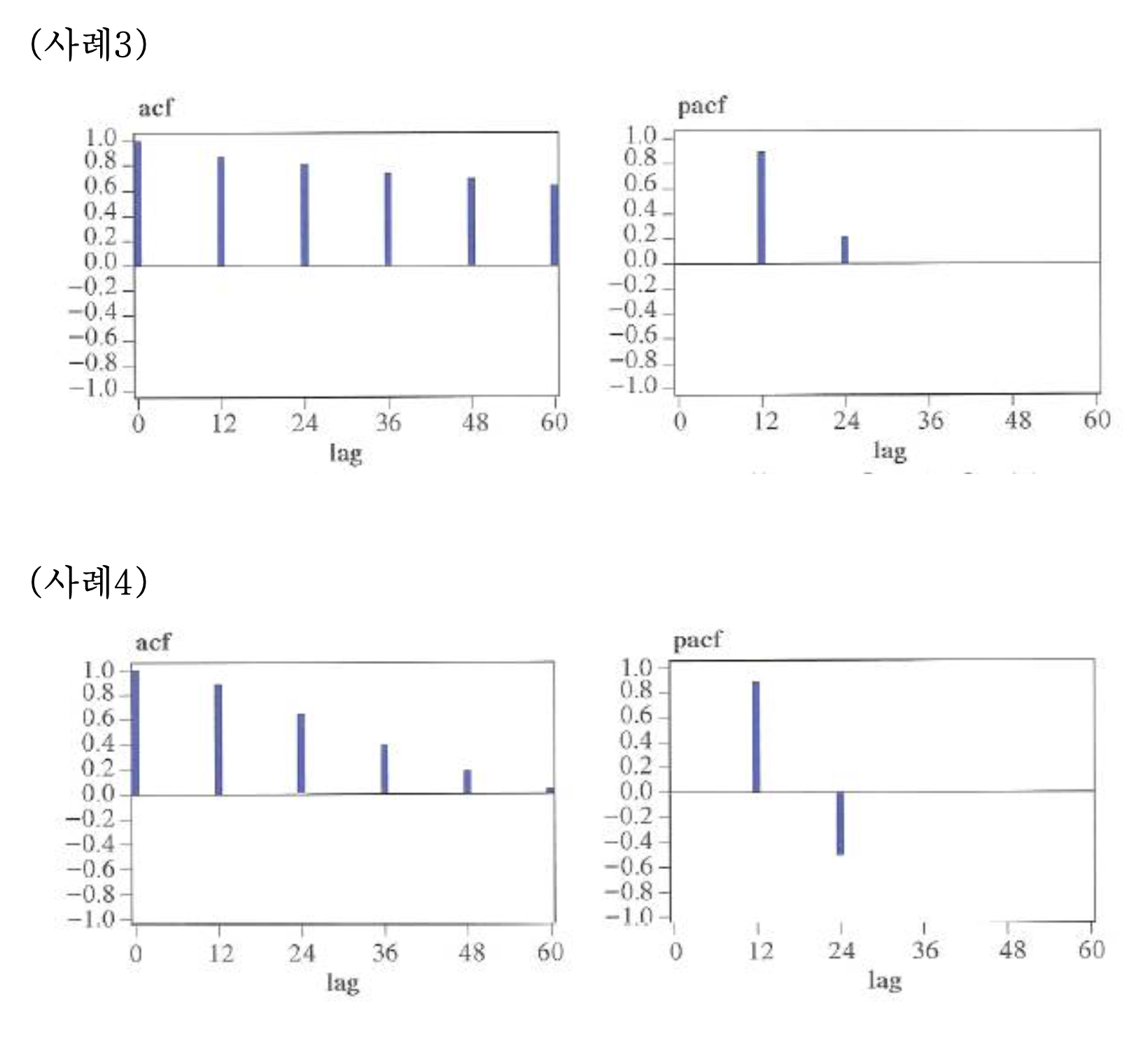
계절 SARMA(1, 1), s=12 모형의 ACF, PACF
- ACF와 PAC 모두 주기가 12이면서 점진적으로 감소하는 패턴을 갖는다.

- 자기상관함수(ACF)는 계절주기 s의 배수를 따라 일정한 형태를 나타내는데 시차 2s부터 지수적으로 감소하는 형태를 갖고, 편자기상관함수(PACF)는 역시 일반 ARMA(1, 1)모형의 편자기상관함수와 같이 시차 2s부터 (부호를 바꿔가면서) 지수적으로 감소한다.
'통계공부 > 시계열분석' 카테고리의 다른 글
| 비정상적계절시계열모형(2) - 혼합계절시계열 (0) | 2021.06.08 |
|---|---|
| Box-Jenkins 모형 (5) - 비정상적 시계열, ARIMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (4) - 시계열의 모형구축 (0) | 2021.06.08 |
| Box-Jenkins 모형 (3) - MA모형, AR모형, ARMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (2) - 정상적 시계열에 대한 Box-Jenkins 모형 (0) | 2021.06.08 |
