계절시계열의 식별
순수계절시계열모형은 현재 시점과 주기 s 간의 관계만을 나타내고 있으므로, 시점 t와 (t-s) 사이에 있는 시점들에서의 변화는 설명하지 못하기 때문에 일반적인 AR 또는 MA모형의 파라미터도 모형에 포함된 혼합형 모형을 찾아야 한다.
가법적 계절모형(가법계절혼합모형)
예를 들어, 일반 AR(1)과 계절 SAR(1)이 혼합된 모형은 다음과 같이 표현한다.

위의 식은 현재 시점(t)의 시계열은 (t-1) 시점과 (t-s) 시점의 시계열자료들의 합으로 표현된 가법계절모형이다. 하지만 가법계쩔모형보다는 승법계절모형이 보다 더 현실적이여서 더 자주 쓰인다.
승법적계절모형(승법계절혼합모형)
(1) 승법계절모형이란 가법계절모형에 일반모형의 시점 (t-1)과 계절시점(t-s)의 교호가 포함된 모형이며, 일반적으로 AR(1)과 SAR(1)의 승법계절모형(승법계절혼합모형)을 일반적으로 다음과 같이 표현한다.

여기서 α1α1*는 새로운 파라미터가 아니고 교호작용을 의미한다.
(2) 일반모형의 시점과 계절모형의 시점이 혼합된 몇 가지 모형들
1) AR(1) X SAR(1) 모형

2) MA(1) X SMA(1) 모형

3) ARMA(1, 1) X SARMA(1, 1) 모형

-> 대부분의 계절시계열은 순수계절시계열이 아니라 일반시차와 계절시차가 혼합된 형태의 혼합모형을 따른다고 보아야 할 것이다.
혼합모형에 대한 ACF의 패턴
(1) MA(1) X SMA(1), s=12 모형


- 일반모형 MA(1)과 계절모형 SMA(1)의 혼합모형으로 시차(1)에서 MA(1)에 따른 ACF가 나타나고 시차(12)에서 SMA(1), s=12에 따른 ACF가 얻어지게 된다
- 시차(11)과 (13)에서도 작은 ACF가 얻어지는데, 여기서 AC(11)이란 물론 Yt와 Yt-11의 상관계수, 즉 AC(11) = Corr(Yt, Yt-11)
- 다음은 MA(1) X SMA(1), s=12 모형의 ACF와 PACF 사례들

(2) MA(2) X SMA(1), s=12 모형
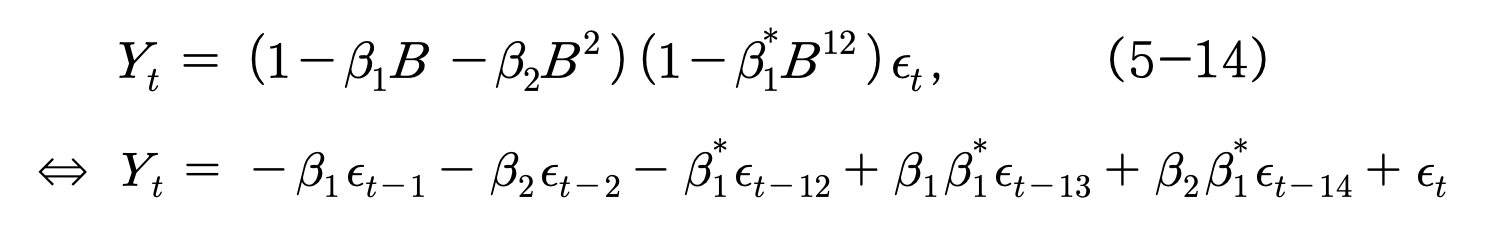

- 일반모형이 MA(2)이므로 시차(1)과 (2)는 MA(2)에 따른 ACF, 계절모형이 SMA(1)이므로 시차(12)에서 SMA(1), s=12에 따른 ACF가 존재한다.
- 그 외의 시차 (10), (11), (13), (14)에서 ACF가 얻어진다.
(3) MA(1) X SMA(2), s=12 모형

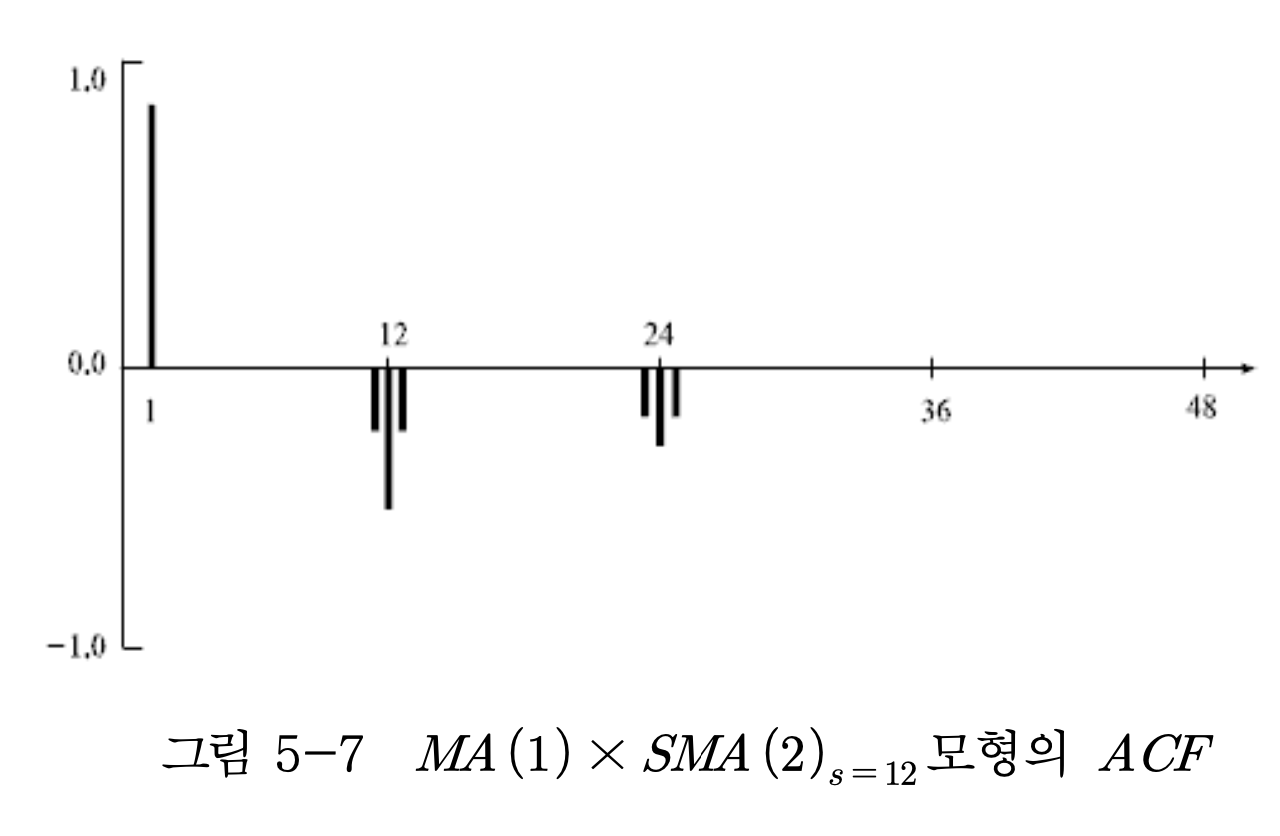
- 일반모형 MA(1)과 계절모형 SMA(2)의 혼합모형으로서, 시차 (1) 에서는 MA(1)으로부터, 시차 (12)와 (24)에서는 SMA(2), s=12 로부터 얻어지는 ACF가 존재한다.
- 그리고 시차 (11), (13)과 시차 (23), (25)에서 spike가 있게 되며, AC(11) = AC(13), AC(23) = AC(25)
(4) MA(2) X SMA(2), s=12 모형
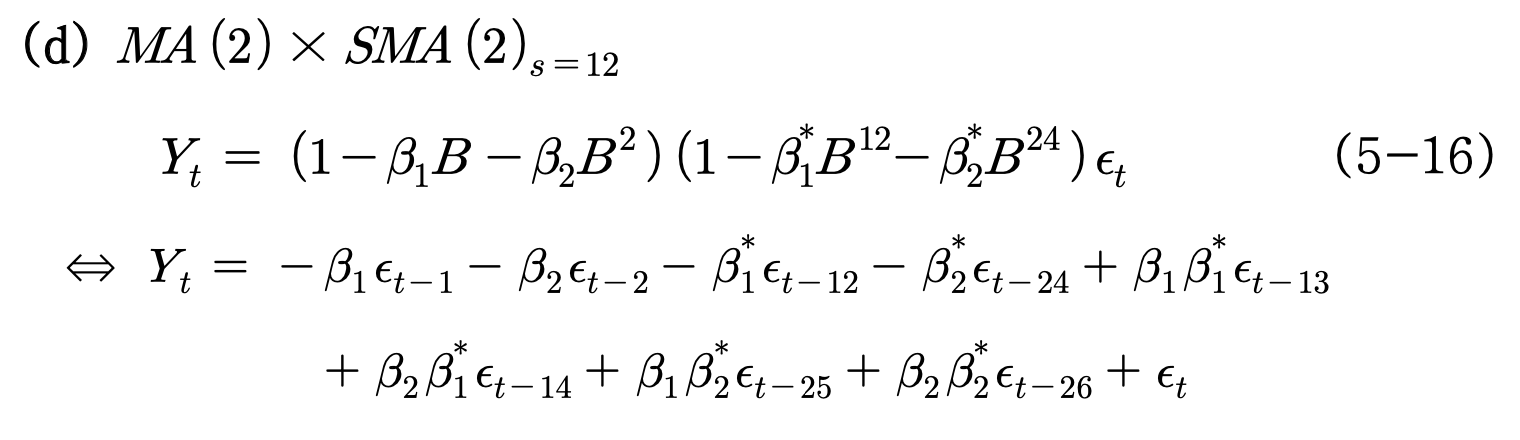

- 시차(1)과 (2)에서 MA(2)로 부터, 시차 (12)와 (24)는 SMA(2), s=12 로부터 얻어지는 ACF들
- 그 밖에 시차 (10), (11), (13), (14)에 대해서 또 시차 (22), (23), (25), (26)에 대해서 ACF의 spike를 볼 수 있다.
(5) MA(2) X SARMA(1, 1), s=12 모형


- MA(1)으로부터 시차(1)의 ACF가 나타나고 SARMA(1, 1), s=12 로부터 시차 (12), (24), (36) 등에서 지수적으로 작아지는 ACF가 얻어진다.
- 시차 (12), (24), (36) 등의 전후 시차에서 비교적 작은 ACF가 얻어짐을 알 수 있다.
- MA(1) X SAR(1), s=12 모형의 ACF와 PACF의 예시
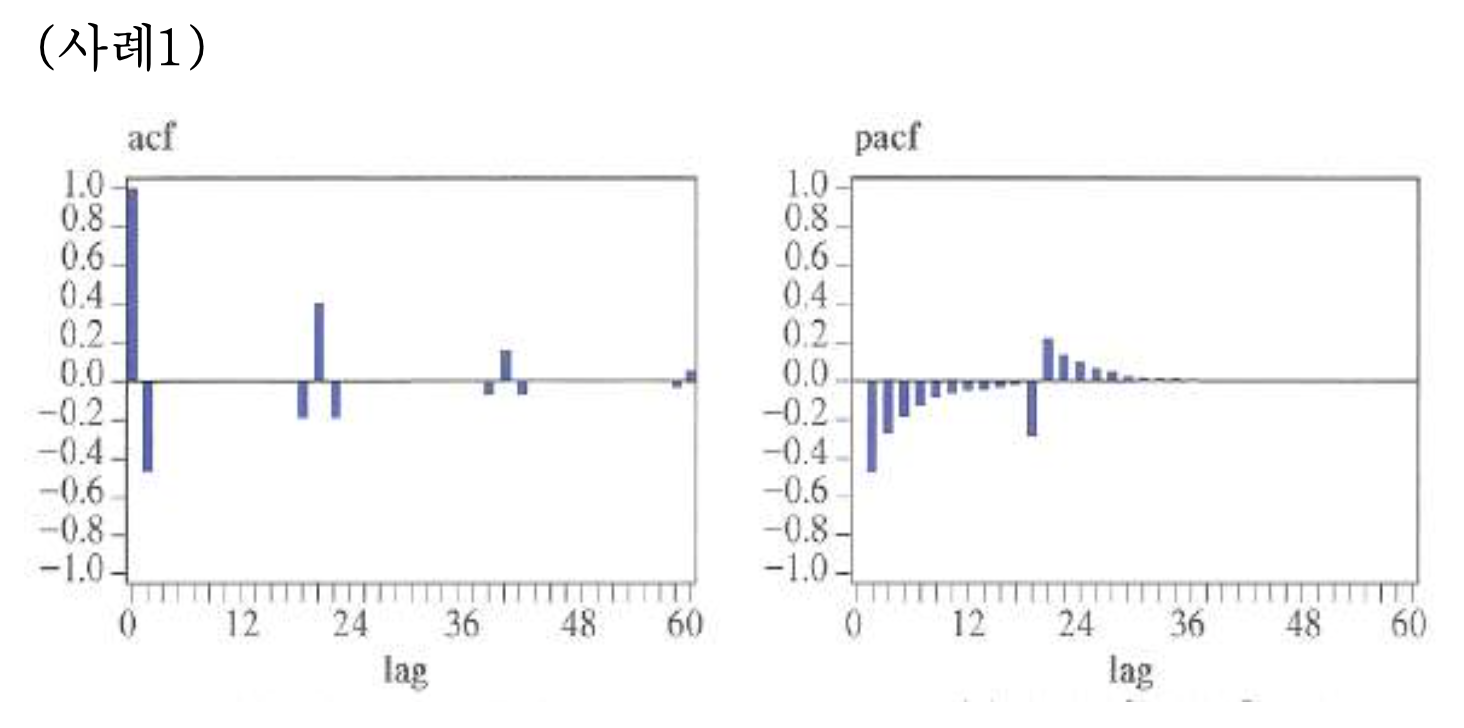

** 각 모형의 ACF들을 이론적으로 계산되는 결과들인데, 실제의 시계열자료에서 계산된 ACF 값들이 앞에서 설명한 것과 정확히는 일치하지 않을 것이다. 따라서 주어진 시계열자료(표본)를 통하여 게산된 ACF값들 중에서 유의적인 것들이 위의 한 그래프와 유사하다면 그 시계열자료는 그 그래프의 해당 모형으로 식별할 수 있다는 것이다.
* 계절시계열의 일반시차와 계절시차가 혼합된 AR모형들에 대해서는 유사한 방법으로 PAC 패턴을 살펴보면 혼합 AR 계절시계열을 식별할 수 있을 것이다.
(6) 그 외의 계절시계열자료로들로 부터 얻은 ACF 예시
1) MA(1) x SMA(1), s=12 모형

2) MA(2) x SMA(1), s=12 모형

3) MA(2) x SMA(1), s=12 모형
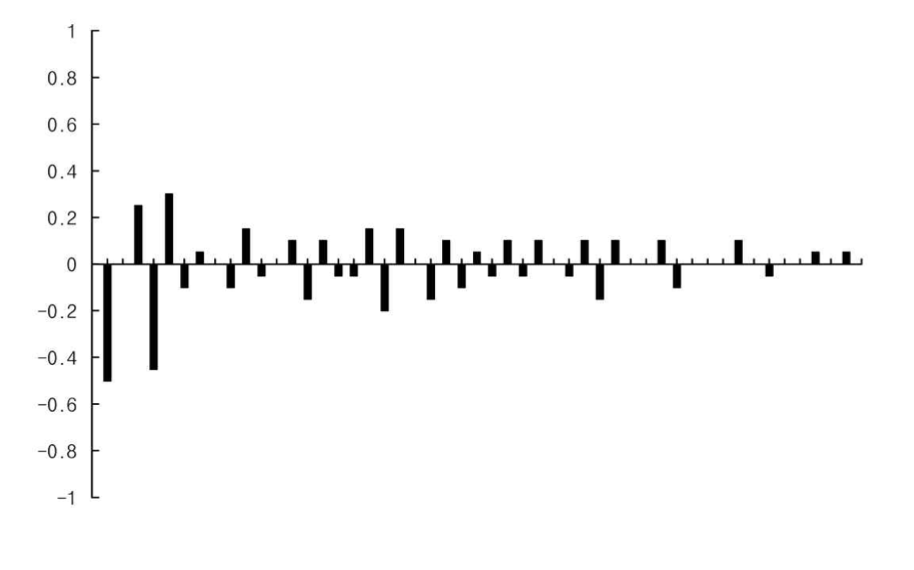
4) MA(1) x SMA(1), s=4 모형

5) MA(1) x SAR(1), s=12 모형 또는 MA(1) x SRMA(1), s=12 모형

-> 위의 (5)에서는 시차(12)에서 spike가 있으며 AR(1)으로 부터 빠르게 작아지는 ACF가 반영된 것이다.
비정상적 계절시계열
일반적으로 비정상적 계절시계열은 정상적 계절시계열이나 계절성이 없는 비정상적시계열과도 매우 다른 복잡한 패턴을 가지고 있는 시계열 자료이며, 따라서 비정상성과 계절성을 동시에 고려해야 한다.
(예) 시계열자료에 추세가 있을 경우 차분을 한다고 설명하였는데, 주기가 4인 계절 시계열이면서 {Y1, Y5, Y9, ... }와 {Y2, Y6, Y10, ... }, ... 등이 각각 서로 다른 추세를 보이는 경우 통상적인 차분만으로 정상적 시계열로 전환되지 않는다.
이때, 비정상적시계열의 주기가 12인 시계열 자료 {Y1, ... , YT}에 대하여 Z(t) = Y(t) - Y(t-12) = (1-B^12)Yt, t= 13, 14, ... , T 라고 하면 Zt를 계절차분된 시계열이라고 한다. 이때 계절차분한 시계열자료에 추세가 존재한다면 Zt를 다시 1차 차분하여 (일반차분)

로 할 때, 비로소 정상적 시계열이 얻어지게 된다. 결국

가 정상적 시계열이 되고 이 시계열에 대해 식별의 과정을 거쳐야 한다는 것이다.
(1) 계절차분과 일반차분이 필요한 시계열자료의 ACF그래프 예1


- 첫 번째 그림은 어느 시계열자료에 대해서 실제로 얻어진 ACF 그래프이며 이 그래프의 형태는 거의 직선에 가깝게 감소(완만하게 감소)하는 모습을 보이기 때문에 차분이 필요해보인다.
- 두 번째 그림은 우선 1차 차분을 했을 경우의 ACF 그래프이며, 이 그래프에서 계절성이 있음을 뚜렷하게 볼 수 있다.(자기상관계수가 일정하게 감소하는 형태). 따라서 이 시계열 자료는 1차의 일반차분과, 주기 12의 계절차분이 필요한 비정상적 시계열자료임을 알 수 있는 것이다.

- 1차차분과 계절차분을 한 후 시계열 자료에 대해서 ACF를 구하면 시차 12에서만 유의적인 ACF가 나타나고 다른 시차들에서는 비유의적인 ACF들이 나타나므로 계절차분과 일반차분을 거친 시계열 자료 (1- B)(1-B^12)Yt는 정상적 시계열로 판단되며, 이 정상적 시계열을 SMA(1), s=12 인 모형으로 식별할 수 있게된다.
(2) 계절차분과 일반차분이 필요한 시계열자료의 ACF그래프 예2

- 어느 시계여자료의 ACF그래프 자체가 계단식으로 감소하고 있기 때문에 계절성(주기 12)이 강하게 있는 비정상적 계절시계열자료임을 알 수 있다.

- 비정상적 계절시계열에 대해 일반차분과 계절차분을 어느 것을 먼저해도 상관이 없다. 따라서 계절차분을 먼저한 경우의 ACF를 구하면 시차가 증가함에 따라 완만하게 감소(직선으로 감소)하는 형태를 보아서 일반차분이 필요한다는 것을 알 수 있다.
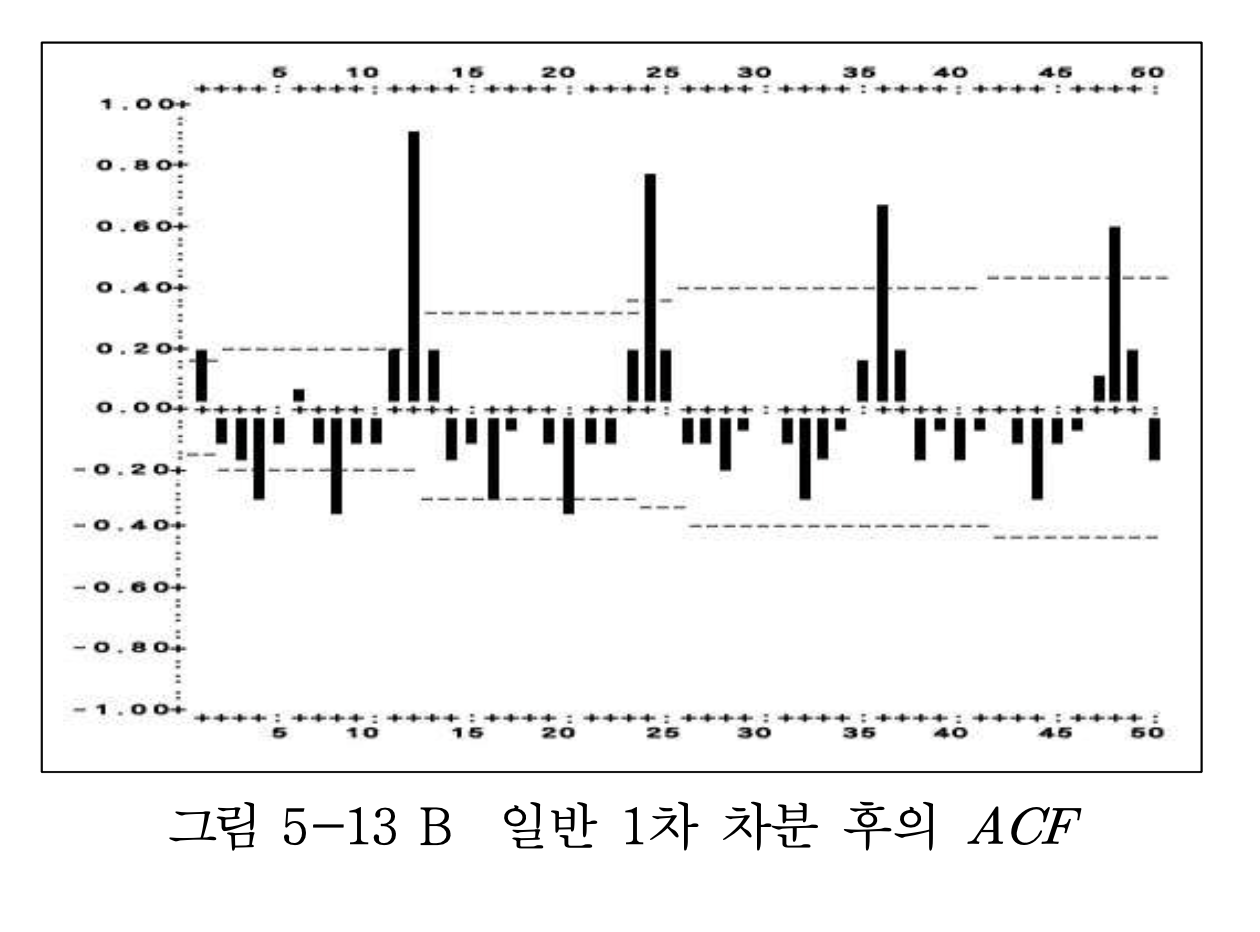
- 마지막으로 일반 1차 차분 후의 ACF을 구해보면 이 시계열은 MA(1) X SAR(1), s=12 로 식별되는 것을 알 수 있다.
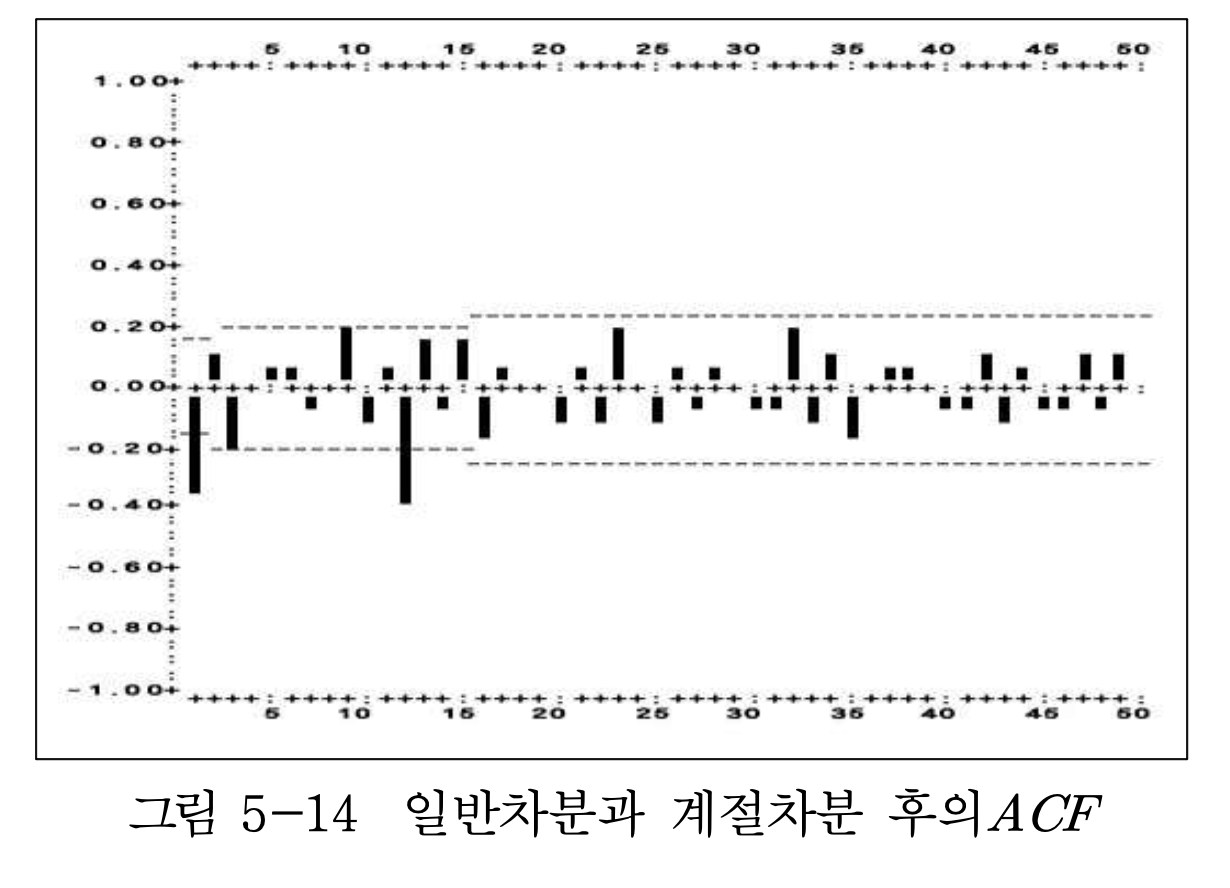
- 다음은 다른 예로, 일반 1차차분과 계절차분 후의 ACF의 그래프를 구하고, 그래프를 확인하면 MA(1) X SMA(1), s=12 로 식별되는 것을 확인할 수 있다.
'통계공부 > 시계열분석' 카테고리의 다른 글
| 비정상적계절시계열모형(1) - 순수계절시계열 (0) | 2021.06.08 |
|---|---|
| Box-Jenkins 모형 (5) - 비정상적 시계열, ARIMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (4) - 시계열의 모형구축 (0) | 2021.06.08 |
| Box-Jenkins 모형 (3) - MA모형, AR모형, ARMA모형 (0) | 2021.06.08 |
| Box-Jenkins 모형 (2) - 정상적 시계열에 대한 Box-Jenkins 모형 (0) | 2021.06.08 |
